급하게임개발

https://www.acmicpc.net/problem/15661

이 문제의 경우 다르게보면 조합이지만 이 문제의 분류가 비스마스킹으로 되어 있어서 비스마스킹으로 풀려구 생각했다
이 문제의 비트마스킹은 총 나는 2개를 사용 했는데 일단 team의 점수를 저장하는데 사용 했다 (이 부분에서 좀더  최적화가 가능하나 귀찮아서 진행 하지않았다) 두번째로는 팀들을  나누는데 비트마스킹을 사용했다.

	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++) {
			cin >> arr[i][j];
			int teamNum = (1 << i) | (1 << j);
			teamP[teamNum] = arr[i][j]+arr[j][i];
		}
	}

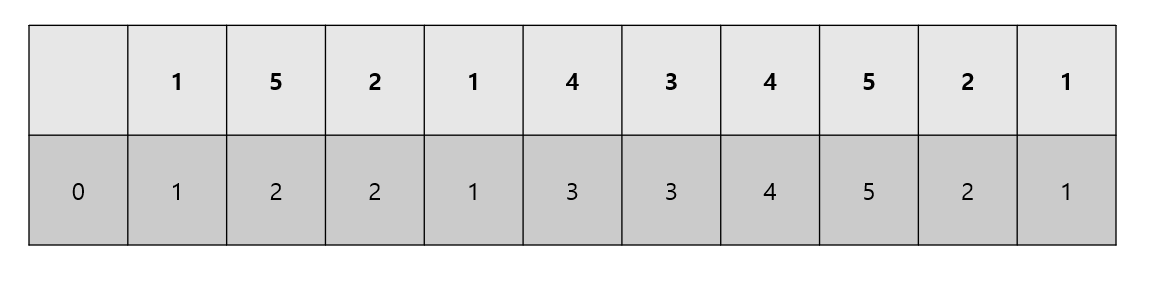
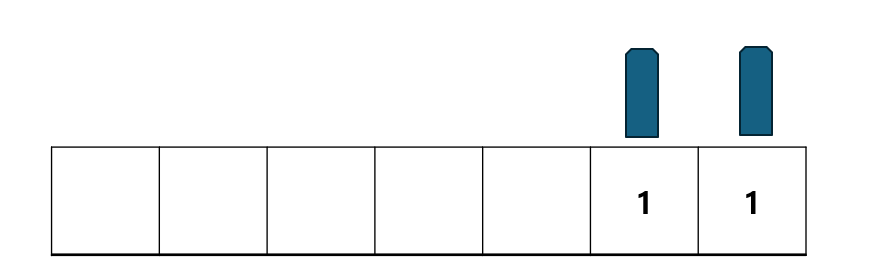
나는 일단 teamP라는 곳에 두명이 차지했을 때의 점수를 넣어줬다 위에처럼 1001일때는 5임으로 4번과 1번팀이 같이 되어있을 때를 나타내며 각팀이 만들어내는 숫자에 따라 점수를 넣어줬다

숫자 일단 이문제의 경우 이렇게 1번팀 0번팀으로 나눌수 있는데 숫자 5의 경우 팀을 위에 그림처럼 나누게 된다

for (int i = 1; i < (1<<n); i++) {
	for (int j = 0; j <= n; j++) {
		if (i & (1 << j))
			team1.push_back(j);
		else
			team2.push_back(j);
	}

이 부분의로직은 이렇게 되는데 i=1부터 시작한다 그  이유는 0번비트만 있을 때는 팀을 만들 수 없으므로 0번 비트  1번 비트 2개가 있는 상황 부터 시작하기 위해서 1번 부터 비트를 사용한다 또한 1<<n 을한 이유는 우리의 테스트 케이스 4를 예시로 들면 비트 4개로 만들수 있는 최댓값은 15인데 1<<4는 16이므로 이부분보다 작을 동안만 우리는 연산을 해주면된다

j변수를 사용하는 루프의 경우는 이제 각비트가 어떤 비트인지 판별하기 위해서 해당 연산을 진행하고 0인지 1인지에 따라 팀에 분배해주게 된다

그후 우리는 두명만이 각 짝을 이뤄 점수가 있으므로

		for (int k = 0; k < team1.size(); k++) {
			for (int p = k + 1; p < team1.size(); p++) {
				sum1 += teamP[(1 << team1[k]) | (1 << team1[p])];
			}
		}
		for (int k = 0; k < team2.size(); k++) {
			for (int p = k + 1; p < team2.size(); p++) {
				sum2 += teamP[(1 << team2[k]) | (1 << team2[p])];
			}
		}

이런 식으로 각 팀의 연산을 해준다

전체 코드는 아래와 같다

#include <iostream>
#include<bitset>
#include<vector>
#include<algorithm>
using namespace std;
int arr[20][20];
vector<int> team1;
vector<int> team2;
int maxresult = 1e9;
int teamP[2097152];
int main() {
	int n;
	cin >> n;
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++) {
			cin >> arr[i][j];
			int teamNum = (1 << i) | (1 << j);
			teamP[teamNum] = arr[i][j]+arr[j][i];
		}
	}
	int sum1 = 0;
	int sum2 = 0;
	
	for (int i = 1; i < (1<<n); i++) {
		for (int j = 0; j <= n; j++) {
			if (i & (1 << j))
				team1.push_back(j);
			else
				team2.push_back(j);
		}
		for (int k = 0; k < team1.size(); k++) {
			for (int p = k + 1; p < team1.size(); p++) {
				sum1 += teamP[(1 << team1[k]) | (1 << team1[p])];
			}
		}
		for (int k = 0; k < team2.size(); k++) {
			for (int p = k + 1; p < team2.size(); p++) {
				sum2 += teamP[(1 << team2[k]) | (1 << team2[p])];
			}
		}
		if (team1.size() && team2.size())
			maxresult = min(maxresult, abs(sum1 - sum2));
		team1.clear();
		team2.clear();
		sum1 = 0;
		sum2=0;
	}

	cout << maxresult;
}

https://www.acmicpc.net/problem/14284

이 문제는 다익스트라 알고리즘을 사용해서 풀 수 있다 현재 이블로그에 있는 다익스트라 알고리즘에 관한 문제는 비슷한 양상을 보인다

void djikstraSolution(int start) {
	int startNode = start;
	int toCost = 0;
	djikstra_pq.push({ startNode,toCost });

	while (!djikstra_pq.empty()) {
		int toVertex = djikstra_pq.top().first;
		int toCost = djikstra_pq.top().second;

		djikstra_pq.pop();

		int distanceToNextVertex = distanceV[toVertex];
		if (distanceToNextVertex < toCost) {
			continue;
		}
		for (int i = 0; i < edgeList[toVertex].size(); i++) {
			// 다음 인덱스로 가는 cost
			int cost = edgeList[toVertex][i].second + toCost;
			// 나를 통해 갈 다음 IDX
			int nextIdx = edgeList[toVertex][i].first;
			if (cost < distanceV[nextIdx]) {
				distanceV[nextIdx] = cost;
				djikstra_pq.push({ nextIdx,cost });
			}
		}


	}
}

이 부분이 핵심 부분인데

1. 일단 start 즉 시작점으로 부터의 거리를 구할 것이기에 Start -> Start의 toCost를 0 start->start의 다음인덱스 start를 우선순위 큐에 넣는다 (우선순위 큐는 값이 작은게 root 에 있다)

2.그리고 우선순위 큐가 빌때 까지 
현재 우선순위 큐에 들어가 있는 버텍스와 경로들을 뽑아서 해당 경로들에  영향을 받는 다른 vertex들의 cost값을 업데이트 해줘야 한다

3.일단 node1 -> node2 로 갈때의  현재 우선순위 큐에들어가 있는 가장 작은 애를 가져온다 그후 내가 node1을 통해서 가는 node2 까지의 거리와 이전부터 업데이트  해놓은 1부터 node2까지의 거리를 비교해서 작은 값일 때  node2를 통해서 가는 거리들의 값을 업데이트 해준다 그후 다음 업데이트를 할수도 있으니 해당 값들을 우선순위 큐에 넣어주고 반복한다

전체 코드는 아래와 같다

#include <iostream>
#include<queue>
using namespace std;
int n, m;

#define INF 1e9+7
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> djikstra_pq;
vector<pair<int, int>> edgeList[5001];
vector<int> distanceV(5001);
void djikstraSolution(int start) {
	int startNode = start;
	int toCost = 0;
	djikstra_pq.push({ startNode,toCost });

	while (!djikstra_pq.empty()) {
		int toVertex = djikstra_pq.top().first;
		int toCost = djikstra_pq.top().second;

		djikstra_pq.pop();

		int distanceToNextVertex = distanceV[toVertex];
		if (distanceToNextVertex < toCost) {
			continue;
		}
		for (int i = 0; i < edgeList[toVertex].size(); i++) {
			// 다음 인덱스로 가는 cost
			int cost = edgeList[toVertex][i].second + toCost;
			// 나를 통해 갈 다음 IDX
			int nextIdx = edgeList[toVertex][i].first;
			if (cost < distanceV[nextIdx]) {
				distanceV[nextIdx] = cost;
				djikstra_pq.push({ nextIdx,cost });
			}
		}


	}
}
int main() {
	cin >> n >> m;
	for (int i = 0; i < m; i++) {
		int temp1, temp2, temp3;
		cin >> temp1 >> temp2 >> temp3;

		edgeList[temp1].push_back({ temp2,temp3 });
		edgeList[temp2].push_back({ temp1,temp3 });

	}
	int start, end;
	cin >> start >> end;

	distanceV.assign(n + 1, INF);
	djikstraSolution(start);

	cout << distanceV[end];
}

https://www.acmicpc.net/problem/11054

이  문제의경우 LIS 를 사용할 줄 알면 쉬운 문제이다
그후 LIS의 값과 뒤의 인덱스부터의 LIS

#include <iostream>
using namespace std;
int arr[1000] = { 0, };
int n;
int ascendingNum[1001];
int descendingNum[1001];
int maxNum=0;
void getAsc() {
	for (int i = 1; i <= n; i++) {
		ascendingNum[i] = 1;
		for (int j = 1; j < i; j++) {
			if (arr[i] > arr[j]) {
				ascendingNum[i]=max(ascendingNum[j] + 1,ascendingNum[i]);
			}
		}
	}
}


void getDsc() {
	for (int i = n; i > 0; i--) {
		descendingNum[i] = 1;
		for (int j = n; j > i; j--) {
			if (arr[i] > arr[j]) {
				descendingNum[i] = max(descendingNum[j] + 1, descendingNum[i]);
			}
		}
	}
}
int main() {
	cin >> n;
	for (int i = 1; i <= n; i++) {
		cin >> arr[i];
	}
	getAsc();
	getDsc();
	for (int i = 1; i <= n; i++) {
		if (ascendingNum[i]+descendingNum[i] > maxNum) {
			maxNum = ascendingNum[i] + descendingNum[i];
		}
	}

	cout << maxNum-1;
}

의 값의 합이 최댓값이 되는 부분을 고른후 -1 해주면 된다 -1을 하는 이유는 해당 방식으로 순열을 고르면 그 범위에서  수가 겹침으로 1개를 빼주는 것이다 41퍼대에서 에러가났는데 그 이유는 dp 배열을 1001로해야하는데 1000으로 해서 틀렸었다

LIS 를 설명 하자면
우리 의 테스트 케이스를 리스트로 넣어보자

이렇게 될것이다 왼쪽 아래에 0을 넣은 이유는 1이전에는 증가하는 수열이 0이기 때문에 넣었다

그리고 1까지 가장 긴  증가하는 순열을 1이다

5일 때는 2이다

자 이제 2일 때를 보자 2일때 가장 증가하는 부분순열은 나 이전에 나보다 작은 애까지의 부분순열의 최댓값을 넣어 주면 된다 즉 나의 이전에 값들중 나보다 작은 값들의 증가하는 부분순열의 최대값들을 더하는 것이다 예시로 더 설명 하도록 하겠다

완성된 그림을 보자 뒤에서 부터 2번째의 5를 보자 얘보다 작은 애들중 가장  큰인덱스는 8번째인덱스의  4이다 해당인덱스의 나를 붙이면 해당 사이즈의 +1이 되기에 5이다

https://www.acmicpc.net/problem/2437

솔직히 이 문제는 못 풀었다 풀이를 보고나서 이해를 할 수 있었다 이 문제의 코드는 그리 길지 않지만 하나의  로직을 아는사람이 풀 수 있었다.  핵심로직은 내가 어떠한 무게추를 들고 있다고 가정하자 일단 1이라는 무게추가 있다고 가정 하자 1이라는 무게추가 있을 때 다음 무게추가 지금 내가 가지고 있는 무게추의 무게보다 크게 되면 사이 무게인 2를 만들 수없다.

다른 예시로 현재 내가 1,1,2 이렇게 총 3개의 무게추를 가지고 있는데 다음 무게추로 6이 들어오게 되면 나는 4를 만들 수  없다

즉 현재 내가 가지고 있는 총 무게추의 무게보다 작은 무게들을 다 만들 수 있을 때 다음에 사용할 무게추는 내가 가지고 있던 총 무게보다 작아야 한다.

해당  로직이 이문제를 풀 수 있게 하는 핵심 로직이었다

#include <iostream>
#include <algorithm>
using namespace std;

int N;
int arr[1000];

int main() {

    cin >> N;
    for (int i = 0; i < N; i++) {
        cin >> arr[i];
    }

    sort(arr, arr + N);

    int res = 1;
    for (int i = 0; i < N; i++) {
        if (arr[i] > res) {
            break;
        }
        res += arr[i];
    }

    cout << res;
}

https://www.acmicpc.net/problem/2170

이 문제는 투 포인터 문제이다 이중 포문으로도 구현이 가능하나 해당 방식으로 할경우 시간 복잡도가 커진다 이에 루프문 한개로 해당 문제를 해결하는 게 핵심이다

이 문제의 로직은 일단 이어지는 선들을 최대한 길게 이어진  후 끊어졌을 때 부터 선을 다시 쭉 길게 이어서 이 선 2개의 길이의 합을 구하는 것이다

주어진 테스트 케이스를 v1.first를 기준으로 정렬하면 해당 그림 처럼 된다. 아래칸은 시작점 위에 칸은 끝나는 점을 의미한다. 이 리스트는 오름차순 정렬을 했다고 가정했기에 첫번째로 나오는 선은 1부터 시작해서 길게 늘일 것이다 즉 첫번째 상태일때

이렇게 된다 그후에 2부터 5까지를 비교했을 때 이 두선은 이어짐으로 start는 그대로 두고 end를 5로 바꿔준다 

그 다음 3부터 5까지도 이 선과 끝점은 같지만 시작점이 다름으로 기존에 있던 선임으로 포함을 시키지 않는다 아직도 start는 1 end 는 5이다
그 후 6과 7을 만났을때는 아래그림처럼 된다

6과 7을 만났을 때는 새  선임으로 기존에 있던 선의 길이를 일단 값을 누적시켜준후 리스틀 끝나지 탐색한후 해당 start와 end값을 다시 더해준다

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int main() {

	ios::sync_with_stdio(0);
	cin.tie(0);
	int n;
	int sum = 0;
	cin >> n;

	vector<pair<int, int>> v;
	for (int i = 0; i < n; i++) {
		int n1, n2;
		cin >> n1>>n2;
		v.push_back({ n1,n2 });
	}
	sort(v.begin(), v.end());
	int start = v[0].first;
	int end = v[0].second;
	for (int i = 1; i < n; i++) {
	

		if (end > v[i].first) {
			end = max(v[i].second, end);
		}
		else {
			sum += end - start;
			start = v[i].first;
			end = v[i].second;
		}

	
	}
	sum += end - start;
	cout << sum;
}

https://www.acmicpc.net/problem/1052

이 문제의 경우 그리디와 비트 마스킹  문제이다 처음에는 while문으로 코드를 작성했으나 해당 문제를 해결 하려했으나 실패 했다. 이에 비트  마스킹을 사용해서 문제를 풀어야 함을 깨달았다. 이 문제를 풀기 위한 생각은 

3리터짜리 물병을 생각해 보면 2리터 물병 하나 1리터 물병이 있다고 가정 하자. 얘를  물병 한개짜리를 만드는 방법은 1리터짜리 물병을 하나더해서 2리터짜리를 만든후 4리터 물병을 만드는 방법이다

즉 이문제를 풀기  위해서는 가장 작은 물병들을 계속 그다음 큰 물병들로 만들면서 진행 해야한다 자 대표적인 예로
2번째 테스트 케이스를 예시로 생각해봅시다

이 문제의 경우 0번째  칸에 있는 1리터짜리 물병을 일단 큰물병으로 만들어보자 1+1 해서 2리터로 만든다 그 후 최소 물병과 다른  물병의 갯수를 저장해놓고 일단  계속 가장 작은 물병을 다음 큰 물병으로 변경시켜 가면서 물병을 합치면서 크기를 늘리면서 갯수를 줄이는 로직이다 그후 최소 물병의  갯수를  만족하면 로직진행을 끝내면 된다

#include<bitset>
#include<iostream>
using namespace std;
int main() {
	int n, k;
	int ans=0;
	cin >> n >> k;
	while (true) {
		int temp = n;
		// 현재 1을 못만났다는 의미
		int firstOnidx = -1;
		//  내가  가지고 있는 물병의 갯수
		int cnt=0;
		// 내가 비교하려는 인덱스의 번호
		int idx = 0;
		
		//현재 물병의 수를 세는 로직
		while (temp) {
			if (temp & 1) {
				if (firstOnidx == -1)
					firstOnidx = idx;
				cnt++;
			}
			idx++;
			//다음 번째 인덱스를 비교하기 위해 오른쪽으로 1칸 이동
			temp >>= 1;
		}
		//
		if (cnt <= k) {
			break;
		}
		else {
			//가장 작은 양이 담겨져 있는 물병을 합쳐서 다음  크기의 물병을 만들기 위함 반복하다보면 원래있던 더큰 크기의 물병과 합쳐지면서 크기가 줄어듬
			n += (1 << firstOnidx);
			//산 물병의  갯수 크기2짜리 물병은 1개짜리 물병 2개 합친것
			ans += (1 << firstOnidx);
		}

		
	}
	cout << ans;
}

https://www.acmicpc.net/problem/13904

이 문제의 경우 그리디 문제이다 이 문제의 경우 Priority Queue로 풀면 쉽게 풀리는  문제였다. 일단 나는 이 문제를 보고 냅색문제 와 비슷 하다고 생각했다. 

일단 나는 이문제의 숙제의 중요도를 숙제의 점수 라고 생각 했다 이에 우선순위 큐에 과제를 끝냈을 때의 점수가 가장 높은것들 순으로 나열 시켰다.

7
4 60
4 40
1 20
2 50
3 30
4 10
6 5

우리의 테스트 케이슬 중요도 즉 과제를 맞췄을 때의 점수를 해당로직대로 내림차순 정렬 하게 되면 아래 그림 처럼 된다

우리가 실제로 과제를 한다 생각 해 보자 우리는 당연히 가장 중요한걸 될 수 있는  한 최대한 미룰 것이다 즉 첫번째 4,60은 아직 4일 차에 내가 할 일이 없으므로 60에 중요도를 가진 과제를 한다.

그후 오는 2,50은 아직 2일차에 아무일도 없으므로 50에 일을 한다 

그 후 4,40의 일은 4일 안에만 하면 되나 4일차에는 60의 일이 있으므로 4일보다 앞에 배정한다 그래서 3일 차에 40의  일을 한다

그후 3,30은 이미 3일차에 40의 일을 하였으니 3일안에 내가 할수 있는 요일은 1일차 밖에 없다 이에 30의 일은 1일 차에 한다

그후 1,20의 일은 이미 1일차에 30의 일을 하니 하지 않는다

그후 4,10의   일도 이미 4일 안에 진행 하는 일들은 다 중요도 가 높으므로 진행 하지않는다
그후 6,5는 6일차는  비어 있으므로 넣는다

즉 이문제의 풀이는 날짜를 최대한 미루데 중요한거를 우선 해서 리스트에 넣어야 한다 이에 만약 내가 4,40의 일을 한다고 가정했을 때 지금 업무를 완료했을 때의점수순으로 나열했기에 후에 나보다 낮은 일수가 나온다고 해도 점수가 높지 않고 일수도 낮고 점수도 낮은게 나올 수가 없으므로 빈공간에 채워주는 식으로 로직을 진행해야 한다

#include<iostream>
#include<queue>
using namespace std;
int day[1001] = {};
struct Compare {
    bool operator()(pair<int, int> const& p1, pair<int, int> const& p2) {
        return p1.second < p2.second;
    }
};
priority_queue<pair<int,int>, vector<pair<int,int>>, Compare> pq;
int main() {
    int N;
    cin >> N;
    int num1, num2;
    int maxIdx=0;
    int result = 0;
    for (int i = 0; i < N; i++) {
        cin >> num1 >> num2;
        if (num1 > maxIdx) {
            maxIdx = num1;
        }
        pq.push({ num1,num2 });
    }

    while (!pq.empty()) {
        int x, y;
        x = pq.top().first;
        y = pq.top().second;
        pq.pop();
        if (day[x]== 0) {
            day[x] = y;
        }
        else {
            for (int i = x - 1; i > 0; i--) {
                if (day[i] == 0) {
                    day[i] = y;
                    break;
                }
            }
        }

    }
    for (int i = maxIdx; i > 0; i--) {
        result += day[i];
    }
    cout << result;
}

https://www.acmicpc.net/problem/9251

이 문제의 경우 DP중에 LCS라는 것에 공부해보았으면 풀 수 있는 문제 였다 처음 보고 나서 부분 순서가 아닌 부분수열로 보아서 틀렸었다 이에 LCS 알고리즘에 대해  공부한 푸니 그리 어렵지 않은 문제였다

#include <iostream>
#include <cstring>
using namespace std;
#define max(a, b) (a > b ? a : b)

int LCS[1002][1002];
char str[1003];
char str2[1003];

int main()
{
	cin >> str >> str2;
	int i, j;
	i = 1;
	while (i <= strlen(str))
	{
		j = 1;
		while (j <= strlen(str2))
		{
			if (str2[j - 1] == str[i - 1])
			{
				LCS[i][j] = LCS[i - 1][j - 1] + 1;
			}
			else
			{
				LCS[i][j] = max(LCS[i - 1][j], LCS[i][j - 1]);
			}
			j++;
		}
		i++;
	}
	printf("%d", LCS[i - 1][j - 1]);
}

맨 처음 

아래 와 같은 표를 만들준다 만들어 주게 되면 7X7 배열이 될텐데 이는 비교하지 않았을 때 에 대한 값 0을 넣어주기 위함이다.

이에 우리가 각 행 마다 채워넣어줄 것은 각각 행까지의 문자들을 열까지의 문자들과 비교했을 때 최대로 나오는 부분 수열의 크기를 넣어줘야한다 이를 바탕으로 다음 수열의 최댓값을 찾을 것이다

즉 C를 열들의 문자와 비교한다 1행 1열이 0인이유는 C를 A까지 비교했을떄 나오는 부분수열이 없기 떄문이다 그후 C를 A C라는 문자열과 비교했을 때 부분수열로 나온것은 C이니 1 지금 집합 C에서의 부분수열이 1밖에 나올수 없으므로 1만채워주게 된다 

그 후 두번째 줄은 C A에서의 부분수열값과 A의 부분수열값을 비교해주게 되는데 C A와 A는 하나의 부분수열 만 공유한다 C A와 A C 도마찬가지이다 C혹은 A만을 공유하기에 1이다 단 이제 C A와 A C A를 비교해주게 되면 현재 C A로 부분수열이 만들어진다 이것은 즉이것은 C만을 비교했을 때 이미 부분수열이 1이었고 그다음 A를 비교했을 때 이부분이 현재 같으므로 이전에  가져왔던 값에 +1을 해주게 된다
그림을 완성 하게 되면 

이런식으로 된다 즉 이  문제를 푸는 핵심은 x축으로의 문자열 과 y축으로 문자열을 비교해서 즉 y 인덱스 까지의 수열에서  행의 문자열들과 몇개가 유사한지를 찾는 것이다 이 부분에서 사용되어야 할게 나의 이전에 문자이다 . 예로 
A C A  와 C A를  비교했다고 가정하자 이미 C를 검사했을 때 x축의 C 의 이후 문자들에서는 무조건 1개의 부분수열이 발생한다는 의미이고  C A와 검사했을 때 C까지 이미 1인 부분수열이 있었으므로 A를 만났을 때  A의 이전까지의 최대 부분수열의 갯수와 지금 일치한 대각선의 값이 +1되게 하여 증가시키는 것이다 즉 A C 와 C를 비교했을 때 이미 1개의 부분수열이 존재함으로 A C A 와 C A 를 비교했을때 +1을 해주게 되는 것이

결국에 이식의 점화식은

LCS[i][j] = LCS[i - 1][j - 1] + 1;

LCS[i][j] = max(LCS[i - 1][j], LCS[i][j - 1]);

이렇게 2개가 되는데 
같은 문자를 발견했을 때는 나의 이전 문자까지  비교했을 때의 최대 부분수열의 구성요소 갯수 +1을 해야함으로 i-1과 j-1인덱스의 값에서 +1을 증가시킨다

반대로 틀릴경우에는 즉 y축에서의 나의 이전의 값을 가져오거나 나까지 비교하기전에 최대 부분수열의 인덱스를 가져오게 된다