급하게임개발

https://www.acmicpc.net/problem/1562

이 문제는 dp 와 비트마스킹을 섞은 문제이다 일단 이문제는 이전
https://www.acmicpc.net/problem/10844

10844번 문제를 풀었을 경우 쉬웠을 것이다

일단 우리는 작은 단계에서 부터 검증을 하자 일단 자릿수가 2일때의 계단수를 구해보자

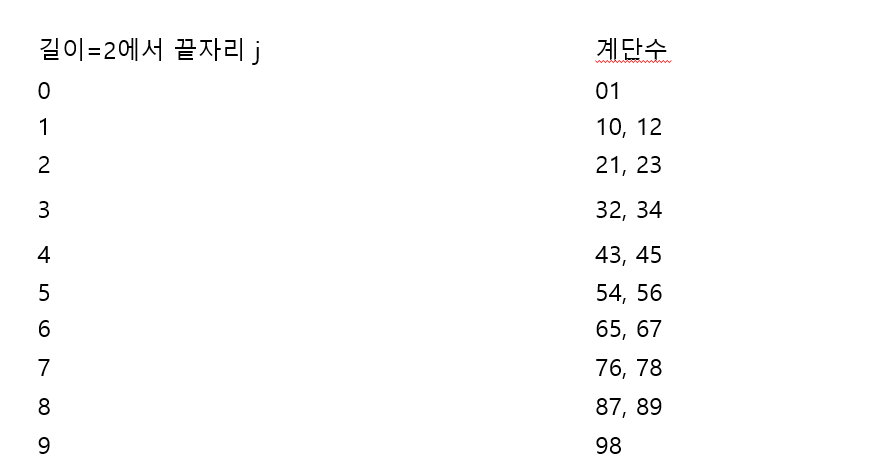
길이 가 3일때는 어떻게 될까 우리는 이전 길이가 2인계단수에서 답을 구할수 있다
자리가 3이고 첫시작수가 2일때 우리는 이전 1과 3에서 값을 가져와서 할수있다 이에

            for (int k = 0; k < 1024; k++) {
                if (dp[i][j][k] == 0) continue;

                int next;
                // 다음 숫자가 j+1일 때
                if (j < 9) {
                    next = k | (1 << (j + 1));
                    dp[i + 1][j + 1][next] = (dp[i + 1][j + 1][next] + dp[i][j][k]) % mod;
                }

                // 다음 숫자가 j-1일 때
                if (j > 0) {
                    next = k | (1 << (j - 1));
                    dp[i + 1][j - 1][next] = (dp[i + 1][j - 1][next] + dp[i][j][k]) % mod;
                }
            }

이렇게 된다 k는 현재 어떤수가 사용되었는지를 비트마스킹으로 나타낸것이다 우리는 이후에 모두 사용된 1023일때만의 값을 구해서 답을 구할 것이다

#include <iostream>
using namespace std;

const int mod = 1e9;
int dp[100][10][1024]; // (자리수, 마지막 숫자, 방문한 숫자 상태)

int main() {
    int n;
    cin >> n;

    // 초기 상태 설정
    for (int j = 1; j <= 9; j++) {
        dp[0][j][1 << j] = 1;  // 첫 번째 자리는 1~9만 가능 (0은 불가능)
    }

    // DP 점화식 수행
    for (int i = 0; i < n - 1; i++) {
        for (int j = 0; j <= 9; j++) {
            for (int k = 0; k < 1024; k++) {
                if (dp[i][j][k] == 0) continue;

                int next;
                // 다음 숫자가 j+1일 때
                if (j < 9) {
                    next = k | (1 << (j + 1));
                    dp[i + 1][j + 1][next] = (dp[i + 1][j + 1][next] + dp[i][j][k]) % mod;
                }

                // 다음 숫자가 j-1일 때
                if (j > 0) {
                    next = k | (1 << (j - 1));
                    dp[i + 1][j - 1][next] = (dp[i + 1][j - 1][next] + dp[i][j][k]) % mod;
                }
            }
        }
    }

    // 정답 계산 (n번째 자릿수에서 0~9까지 모든 숫자를 포함하는 경우)
    int answer = 0;
    for (int j = 0; j <= 9; j++) {
        answer = (answer + dp[n - 1][j][1023]) % mod;
    }

    cout << answer << endl;
    return 0;
}

https://www.acmicpc.net/problem/1939

이 문제는 bfs에 이분탐색을 통한 적절한 값 찾기 이다 
처음에는 갈수있는 경로별 최댓값을 구하려 했으나 시간초과가 났다 당연한 얘기다

자 일단 이코드는 bfs를 통해 특정 노드에서 노드로 가는 경우의 수를 모두 탐색하는데 이때 우리는 무게를 계속 정해주고 해당 무게가 특정 다리의 cost를 넘어가면 이후 탐색의 값을 좀더 줄여 나가는 방식으로 진행한다 도착점에 도착하면 그이후로 탐색하지않는다

#include <iostream>
#include <vector>
#include <queue>
using namespace std;
int n, m;
vector < pair < int , int >> v[100001];
bool isVisited[100001];
int maxNum = 1000000000;
int bfs(int from, int to) {
	int lo = 1;
	int hi = maxNum;
	int mid;
	int ans;
	while (lo <= hi) {
		mid = (lo + hi) / 2;

		for (int i = 0; i < n+1; i++) {
			isVisited[i] = false;
		}

		queue<int> q;

		q.push(from);
		isVisited[from] = true;
		bool canMore = false;

		while (!q.empty()) {
			int node = q.front();
			q.pop();

			if (node == to) {
				canMore = true;
				break;
			}

			for (int i = 0; i < v[node].size(); i++) {
				int next = v[node][i].first;
				int cost = v[node][i].second;
				if (isVisited[next])
					continue;
				if (mid > cost)
					continue;
				isVisited[next] = true;
				q.push(next);
			}
		}

		if (canMore) {
			lo = mid + 1;
			ans = mid;
		}
		else {
			hi = mid - 1;
		}
	}
	return ans;

}
int main() {
	iostream::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);
	cin >> n >> m;
	int a, b, c;
	for (int i = 0; i < m; i++) {
		cin >> a >> b >> c;

		v[a].push_back({ b,c });
		v[b].push_back({ a,c });
	}

	int from, to;
	cin >> from >> to;
	int ans = bfs(from, to);
	cout << ans;

}

이 문제는 유니온 파인드 문제이다 이전 게시글에 크루스칼 알고리즘을 사용하면 쉽게 풀린다

#include <iostream>
#include <queue>
using namespace  std;
int n;
int parent[1000];
priority_queue < pair<long long , pair<int, int >> , vector < pair<long long, pair<int, int>>>, greater<pair<long long, pair<int, int>>> > inputData;

int findParent(int x) {
	if (parent[x] == x)
		return x;
	else
		return parent[x] = findParent(parent[x]);
}

void uni(int x, int y) {
	int parentX = findParent(x);
	int parentY = findParent(y);
	parent[parentY] = parentX;
}

bool isSameParent(int x, int y) {
	int parentX = findParent(x);
	int parentY = findParent(y);
	if (parentX == parentY)
		return true;
	else
		return false;
}

int main() {
	cin >> n;
	int tmp;
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++) {
			cin >> tmp;
			if (i == j)
				continue;
			inputData.push({ tmp,{i,j} });
		}
	}
	for (int i = 0; i < n; i++) {
		parent[i] = i;
	}
	long long ans = 0;
	while (!inputData.empty()) {
		int from = inputData.top().second.first;
		int to = inputData.top().second.second;
		int cost = inputData.top().first;
		inputData.pop();
		if (!isSameParent(from, to)) {
			uni(to, from);
			ans += cost;
		}
	}
	cout << ans;
}

https://www.acmicpc.net/problem/2143

이 문제는 일단 누적합을 이용해서 구간들의 합을 구해야 하는데 구간합간의 단순 비교를 하면 시간 초과가 뜨기 때문에 이문제의 경우 일단 한 배열의  구간 합들을 따로 저장 해놓고  이를 정렬한 후 이분탐색으로 그값의 하위 인덱스와 상위인덱스의 차를 더해주면 된다

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
vector<int> valOfA;
vector<int> valOfB;
vector<int> cmpB;
int main() {
	cin.tie(NULL);
	cout.tie(NULL);
	iostream::sync_with_stdio(false);
	int t;
	int n, m;
	cin >> t;
	cin >> n;
	valOfA.resize(n + 1,0);
	int tmp;
	for (int i = 1; i <= n; i++) {
		cin >> tmp;
		valOfA[i] = tmp + valOfA[i - 1];
	}
	cin >> m;
	valOfB.resize(m + 1, 0);
	for (int i = 1; i <= m; i++) {
		cin >> tmp;
		valOfB[i] = tmp+ valOfB[i - 1];
	}

	for (int i = 0; i <= m; i++) {
		for (int j = i+1 ; j <= m; j++) {
			cmpB.push_back(valOfB[j] - valOfB[i]);
		}
	}
	sort(cmpB.begin(), cmpB.end());
	int start = 1;
	int subAarr = 0;
	long long ans = 0;
	for (int i = 0; i <= n; i++) {
		for (int j = i + 1; j <= n; j++) {
			subAarr =valOfA[j] - valOfA[i];
			subAarr = -(subAarr)+t;
			int lowIdx = lower_bound(cmpB.begin(), cmpB.end(),subAarr) - cmpB.begin();
			int upIdx = upper_bound(cmpB.begin(), cmpB.end(), subAarr) - cmpB.begin();
			ans += upIdx - lowIdx;
		}
	}
	cout << ans;

}

https://www.acmicpc.net/problem/1005

이 문제는 위상 정렬 입니다
근데 일반 위상정렬 하고 다르게 cost 값을 갱신 해주어야 했습니다 어찌 보면 플로이드 워셜하고 비슷 하다고 볼수 있습니다
일단 점입 차수가 0인것부터 큐에 넣고 next들을 갱신해 줍니다 next들은 이전애들이 다 되어야하기 때문에 플로이드 워셜처럼 최단이 아닌 최장을 저장하고 있어야 했습니다

#include <iostream>
#include <vector>
#include <queue>
using namespace std;
int t;
int main() {
	cin >> t;
	int n, k;
	for (int i = 0; i < t; i++) {
		cin >> n >> k;
		vector<vector<int>> inputData(n+1);
		vector<int> cost;
		vector<int> resultCost;
		int inCount[1001] = { 0, };
		int tmp1, tmp2;
		cost.resize(n + 1);
		resultCost.resize(n + 1);

		for (int i = 1; i<= n; i++) {
			cin >> cost[i];
			resultCost[i]=cost[i];
		}
		for (int i = 0; i < k; i++) {
			cin >> tmp1 >> tmp2;
			inputData[tmp1].push_back(tmp2);
			inCount[tmp2]++;
		}

		queue<int> q;
		for (int i = 1; i <= n; i++) {
			if (inCount[i] == 0) {
				q.push(i);
			}
		}
		while (!q.empty()) {
			int cur = q.front();
			q.pop();
			for (int i = 0; i < inputData[cur].size(); i++) {
				int next = inputData[cur][i];
				inCount[next]--;
				if (resultCost[cur] + cost[next] > resultCost[next]) {
					resultCost[next] = resultCost[cur] + cost[next];
				}
				if (!inCount[next]) {
					q.push(next);
				}
			}
		}
		int w;
		cin >> w;
		cout << resultCost[w] << endl;
	}
}

https://www.acmicpc.net/problem/10775

이제 백준 티어가 3  넘어가면서 부터 알고리즘이 하나만 쓰이는게 아니라 여러개 가 섞여 쓰이는게 보이기 시작한다 이문제의 경우 일단 그리디 적으로 하기위해서는 내가 들어갈 수 있는 애중에 가장 큰곳에 들어가야 한다 그러면 내가 들어갈 수 있는곳중 큰곳을 어떻게 구할까가 문제인데 이부분을 유니온 파인드로 만들어 줘야한다.
즉 우리는 비행기들의 그룹을 만들어 줘야한다

해당 인풋을 예시로 생각해 보자
현재 게이트는 1번 2번 3번 4번 이있다
4번 비행기는 4번에 들어가는게 가장 알맞다 그 이후는 이후에 들어올 비행기들이 작을 경우에 작은 비행기들이 들어갈 확률이 적기 때문이다

이에 4 이상의 번호인 비행기들이 다음에 들어갈 수 있는 영역인 3번 비행기의 영역과 묶는 다 만약에 이전에 3번 이하 비행기가 들어와있으면 3번 비행기그룹도 이미 만들어 져있을 것이니까 유니온 파인드를 통해 해당 그룹을 묶어준다

#include<iostream>
#include<algorithm>
using namespace std;
int parent[100000];
int arr[100000];
int g, p;
int Find(int x) {
	if (parent[x] == x)
		return x;
	else
		return parent[x] = Find(parent[x]);
}

void Union(int x, int y) {
	int parentX = Find(x);
	int parentY = Find(y);
	if (parentX > parentY) {
		swap(parentX, parentY);
	}
	parent[parentY] = parentX;
}
int main() {
	cin.tie(NULL);
	cout.tie(NULL);
	ios::sync_with_stdio(false);
	cin >> g;
	cin >> p;
	int n;
	int answer = 0;
	for (int i = 0; i < p; i++) {
		cin >> arr[i];
	}
	for (int i = 1; i <= g; i++) {
		parent[i]=i;
	}

	for (int i = 0; i < p; i++) {
		int f = Find(arr[i]);
		if (f != 0) {
			Union(f - 1, f);
			answer++;
		}
		else {
			break;
		}
	}

	cout << answer;
}

https://www.acmicpc.net/problem/7453

이 문제의 경우 처음에 투포인터로 분류가 되어있어 풀려고 했는데 투포인터가 불가능 하게 리스트가 4개 있어서 안될거 같다는 생각을 했다 그래서 투포인터를 사용하기 위해서는 어떻게 해야할까라고 생각해봤을 때 a와 b의 합을 c와 d의 합의 모든 경우의 수로 리스트를 만들려고 하였다

즉 c와 d의 합을

	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++) {
			cmp.push_back(v[2][i] + v[3][j]);
		}
	}

이런 식으로 만들어 주고

a와 b의 합의 -  를 붙인거가 c와 d를 합친 cmp에 있는 갯수를 더해서 경우의 수를 구하면 된다 근데 갯수를 어떻게 구할지를 생각해보면 -(a+b) 에 대한 거를 algorithm 헤더에 있는 lower_bound와 upper_bound를  이분 탐색으로 해당 수를 찾아 낮은 인덱스 와 높은 인덱스를 찾아 차이가 해당 수의 갯수이니 이를 더해주면 된다.

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
vector<int> v[4];
vector<int> cmp;
long long ans = 0;
int n;
int main() {
	cin >> n;
	for (int i = 0; i < 4; i++) {
		v[i].resize(n + 1);
	}
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < 4; j++) {
			cin >> v[j][i];
		}
	}
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++) {
			cmp.push_back(v[2][i] + v[3][j]);
		}
	}

	sort(cmp.begin(), cmp.end());

	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++) {
			int tmp = v[0][i] + v[1][j];
			int lowIdx = lower_bound(cmp.begin(), cmp.end(), -tmp)- cmp.begin();
			int upIdx = upper_bound(cmp.begin(), cmp.end(), -tmp) - cmp.begin();
			ans += (upIdx - lowIdx);
		}
	}
	cout << ans;
}

https://www.acmicpc.net/problem/9252

이 문제는 전형 적인 dp 문제 였다 

어느 문자를 다른 문자의 n번째 문자의 이전 문자까지의 가장 긴 LCS를 구하는 문제이다

#include <iostream>
#include <string>
#include <vector>
#include <algorithm>
using namespace std;

int arr[1001][1001]; // 배열 크기 수정
string s1, s2;
vector<char> lcsV; // LCS 결과 문자열 저장

void lcsF() {
    int sizeOfs1 = s1.size();
    int sizeOfs2 = s2.size();

    // DP 배열 채우기
    for (int i = 1; i <= sizeOfs1; i++) {
        for (int j = 1; j <= sizeOfs2; j++) {
            if (s1[i - 1] == s2[j - 1]) {
                arr[i][j] = arr[i - 1][j - 1] + 1;
            }
            else {
                arr[i][j] = max(arr[i - 1][j], arr[i][j - 1]);
            }
        }
    }

    // 역추적하여 LCS 문자열 구성
    int i = sizeOfs1, j = sizeOfs2;
    while (i > 0 && j > 0) {
        if (s1[i - 1] == s2[j - 1]) {
            lcsV.push_back(s1[i - 1]);
            i--;
            j--;
        }
        else if (arr[i - 1][j] > arr[i][j - 1]) {
            i--;
        }
        else {
            j--;
        }
    }
    reverse(lcsV.begin(), lcsV.end()); // LCS 문자열을 올바른 순서로 변경
}

int main() {
    cin >> s1 >> s2;

    lcsF();

    // LCS 길이 출력
    cout << arr[s1.size()][s2.size()] << endl;

    // LCS 문자열 출력
    for (char c : lcsV) {
        cout << c;
    }
    cout << endl;

    return 0;
}