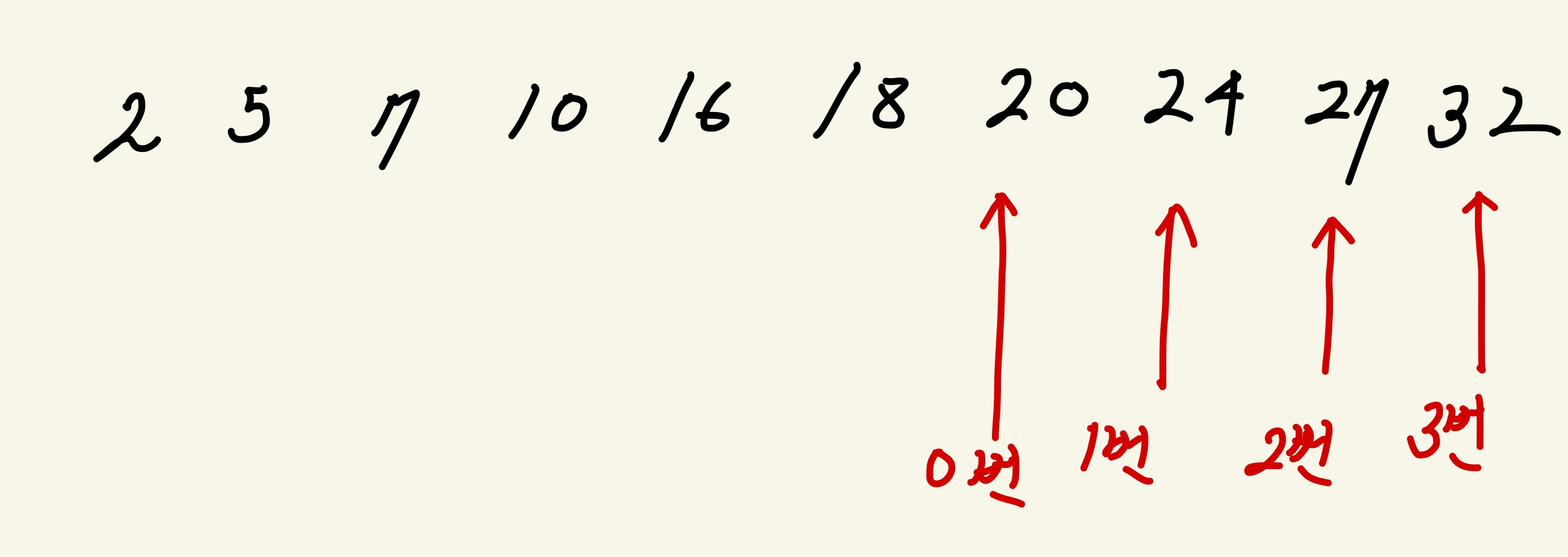https://www.acmicpc.net/problem/12738
이 문제는 내가 투포인터에 넣어놓은 LIS 문제에 이분탐색 버전이다 이전에 어떠한 코테 시험에서 봤을 때 LIS를 투포인터로 풀어서 시간 초과가 히든 테케에서 발생했었는데 이 방식으로 풀었어야 한거 같다

백준 에서 제공 하는 해당 테스트케이스를 예로 들어보자
일단 LIS를 저장하는 LIS 배열이 있다고 생각하자.
LIS 배열이 비었을 때 10을 넣을 수 가 있다
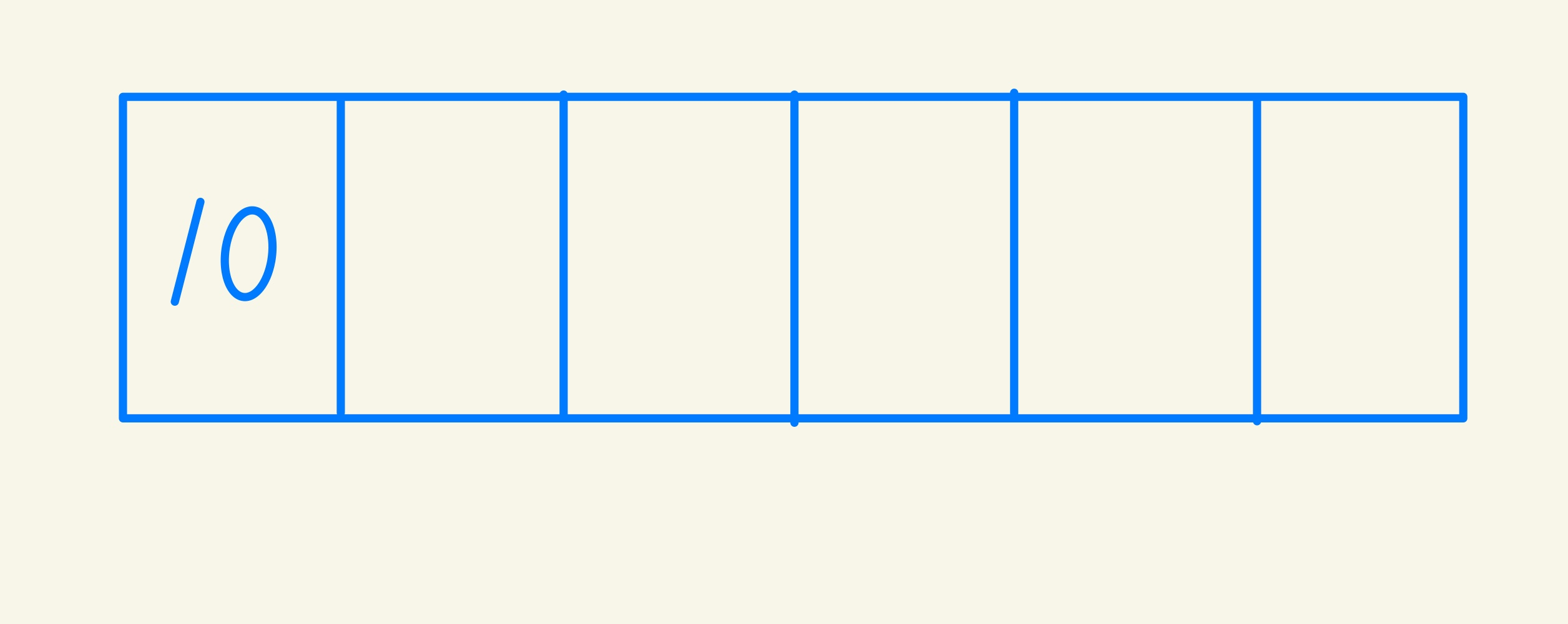
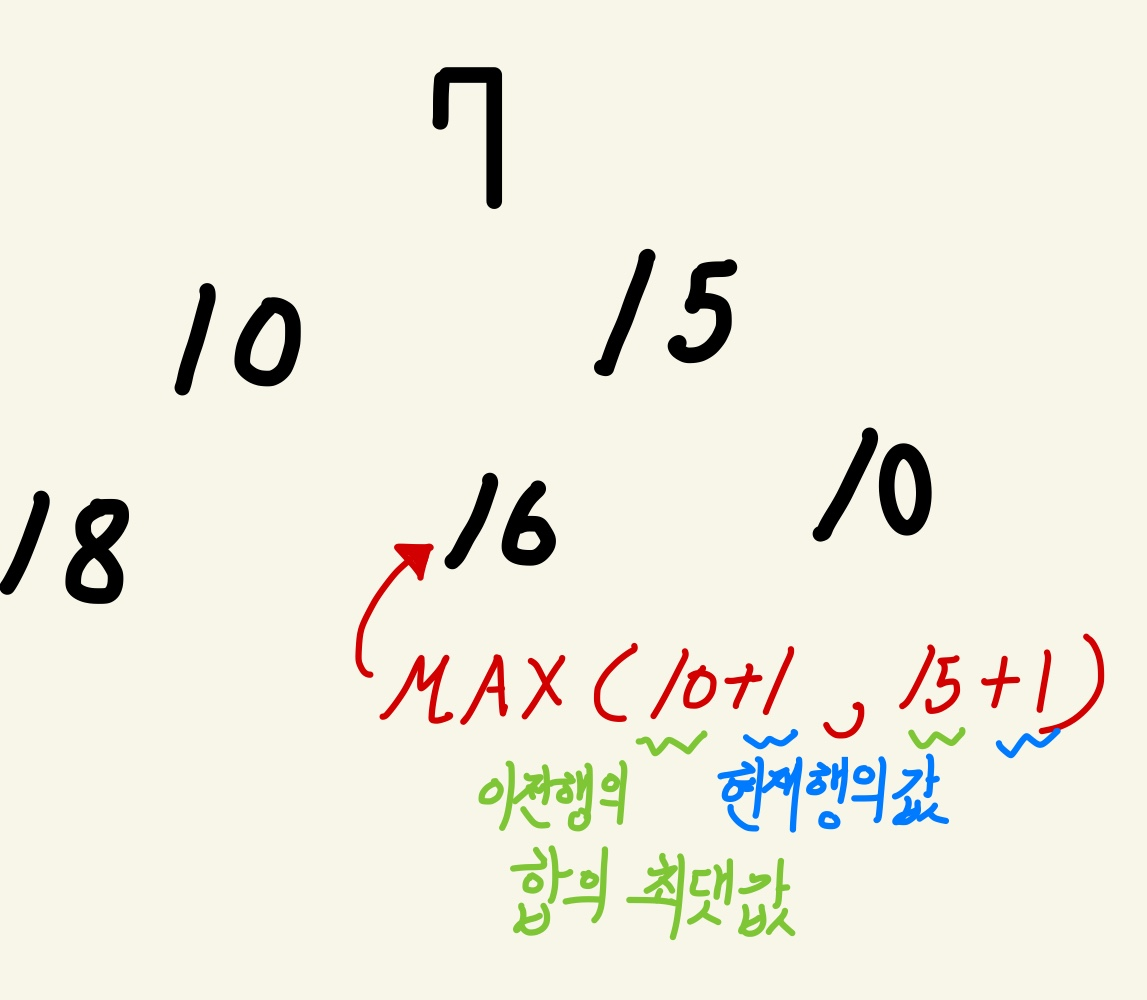
이렇게 되어있는 상황에서 20을 넣는다고 가정할 때 현재 10만 들어가 있는 LIS에서 가장 큰원소이자 마지막 원소인 10보다 20이 크기 떄문에 LIS 배열의 다음 인덱스에 20을 넣어준다

자 그후 10을 넣으려고 보면 10이 들어갈 자리는 10 과 20중에 자기 와 같은 크기의 원소인 10밖에 없다
그럼 으로 해당 10을 최근에 10으로 바꾼다
그후 30을 넣게 되면
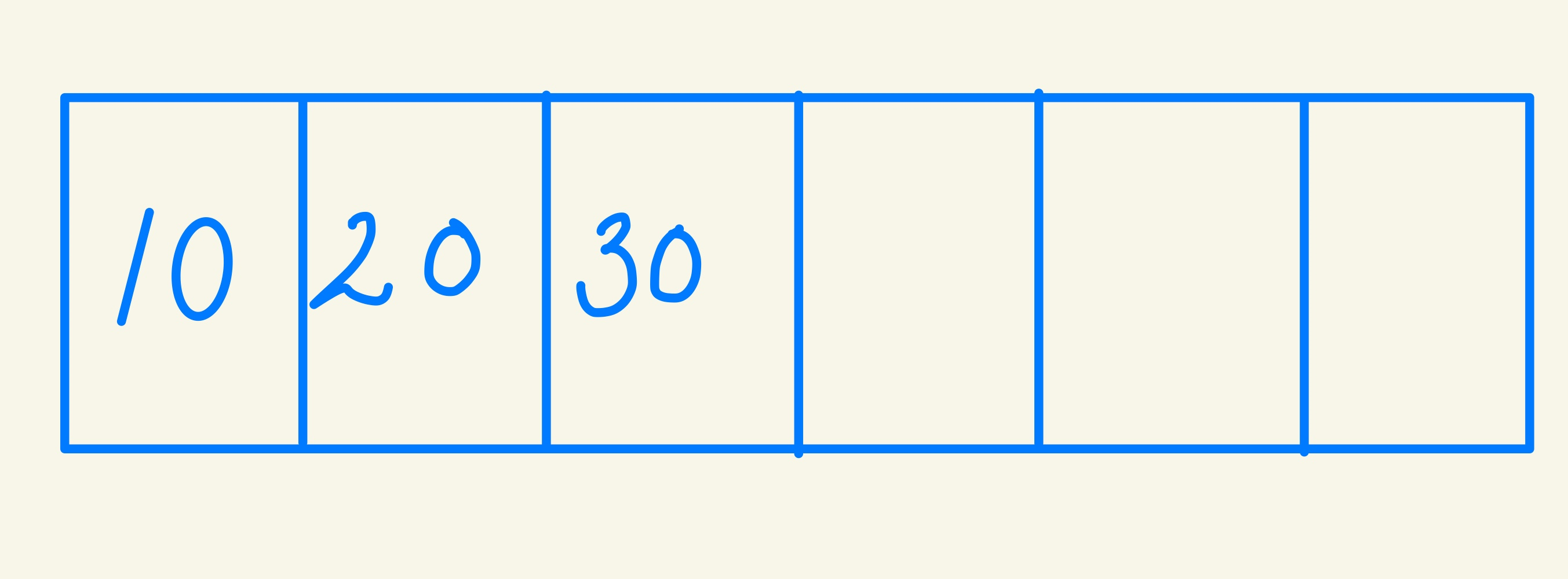
자 이과정을 반복하면 우리는 LIS의 크기를 구할 수 있다
이문제를 풀때의 핵심은
1. LIS 배열이 비었을 때 그냥 원소 넣기
2. LIS 에 있는 원소보다 현재 집어넣을 원소가 클때 끝에 넣기
3. LIS 에 마지막원소(가장큰 원소) 보다 작을 떄 이분탐색으로 들어가야 할 위치 찾아서 넣기
이렇게 하면 결국에 LIS 배열의 크기는 LIS의 크기만큼만 된다
#include <iostream>
using namespace std;
int n;
int arr[1000000];
int lis[1000000];
int binarySearch(int left, int right, int target) {
int mid = 0;
while (left < right) {
mid = (left + right) / 2;
if (lis[mid] < target) {
left = mid + 1;
}
else {
right = mid;
}
}
return right;
}
int main() {
cin >> n;
for (int i = 0; i < n; i++) {
cin >> arr[i];
}
int j = 0;
int i = 1;
lis[0] = arr[0];
while (i < n) {
if (lis[j] < arr[i]) {
lis[j + 1] = arr[i];
j += 1;
}
else {
int pos = binarySearch(0, j, arr[i]);
lis[pos] = arr[i];
}
i += 1;
}
cout << j + 1;
}'백준(코테준비) > 이분탐색' 카테고리의 다른 글
| 백준 1939 (0) | 2025.02.02 |
|---|---|
| 백준 2143 / CPP / 이분탐색 / 누적합 (0) | 2025.01.27 |
| 백준 7453 / C++ / 이분탐색 / 투포인터 (0) | 2025.01.24 |
| 백준 1253 / CPP / 이분탐 (0) | 2025.01.13 |
| 백준 3079/ c++ (0) | 2024.10.21 |