https://www.acmicpc.net/problem/14284
이 문제는 다익스트라 알고리즘을 사용해서 풀 수 있다 현재 이블로그에 있는 다익스트라 알고리즘에 관한 문제는 비슷한 양상을 보인다
void djikstraSolution(int start) {
int startNode = start;
int toCost = 0;
djikstra_pq.push({ startNode,toCost });
while (!djikstra_pq.empty()) {
int toVertex = djikstra_pq.top().first;
int toCost = djikstra_pq.top().second;
djikstra_pq.pop();
int distanceToNextVertex = distanceV[toVertex];
if (distanceToNextVertex < toCost) {
continue;
}
for (int i = 0; i < edgeList[toVertex].size(); i++) {
// 다음 인덱스로 가는 cost
int cost = edgeList[toVertex][i].second + toCost;
// 나를 통해 갈 다음 IDX
int nextIdx = edgeList[toVertex][i].first;
if (cost < distanceV[nextIdx]) {
distanceV[nextIdx] = cost;
djikstra_pq.push({ nextIdx,cost });
}
}
}
}
이 부분이 핵심 부분인데
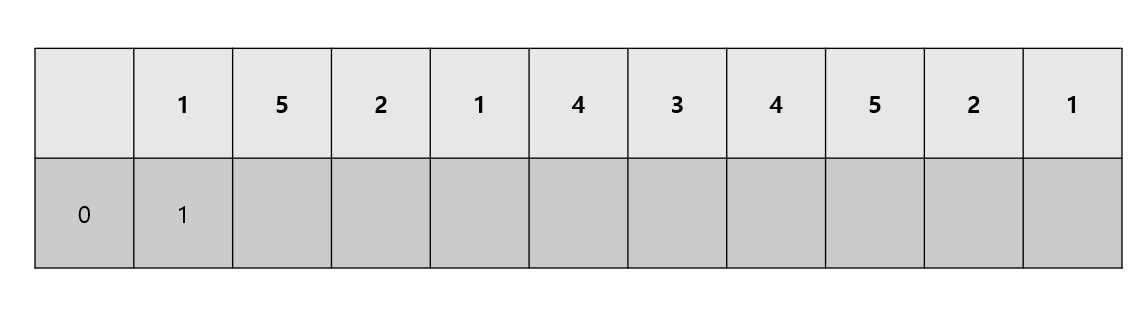
1. 일단 start 즉 시작점으로 부터의 거리를 구할 것이기에 Start -> Start의 toCost를 0 start->start의 다음인덱스 start를 우선순위 큐에 넣는다 (우선순위 큐는 값이 작은게 root 에 있다)
2.그리고 우선순위 큐가 빌때 까지
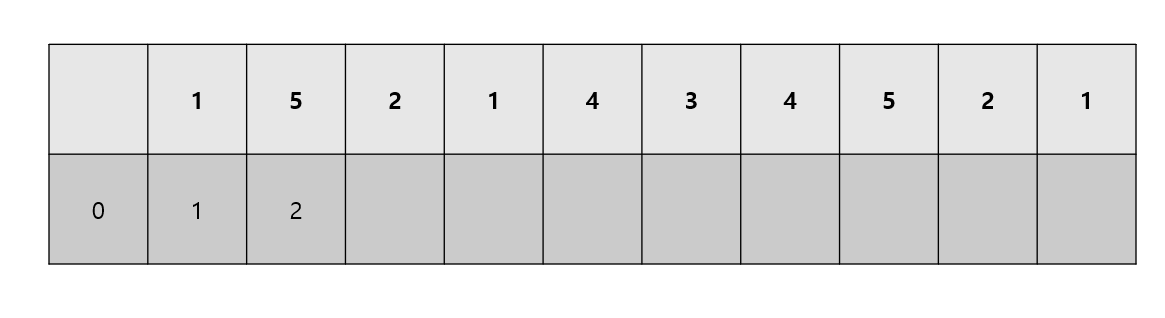
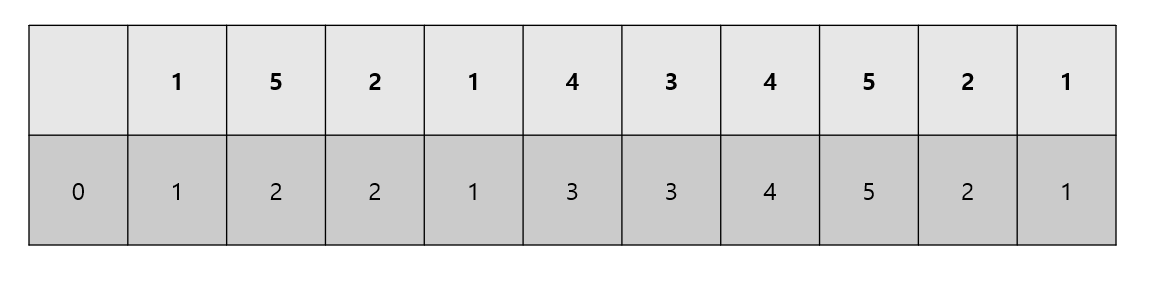
현재 우선순위 큐에 들어가 있는 버텍스와 경로들을 뽑아서 해당 경로들에 영향을 받는 다른 vertex들의 cost값을 업데이트 해줘야 한다
3.일단 node1 -> node2 로 갈때의 현재 우선순위 큐에들어가 있는 가장 작은 애를 가져온다 그후 내가 node1을 통해서 가는 node2 까지의 거리와 이전부터 업데이트 해놓은 1부터 node2까지의 거리를 비교해서 작은 값일 때 node2를 통해서 가는 거리들의 값을 업데이트 해준다 그후 다음 업데이트를 할수도 있으니 해당 값들을 우선순위 큐에 넣어주고 반복한다
전체 코드는 아래와 같다
#include <iostream>
#include<queue>
using namespace std;
int n, m;
#define INF 1e9+7
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> djikstra_pq;
vector<pair<int, int>> edgeList[5001];
vector<int> distanceV(5001);
void djikstraSolution(int start) {
int startNode = start;
int toCost = 0;
djikstra_pq.push({ startNode,toCost });
while (!djikstra_pq.empty()) {
int toVertex = djikstra_pq.top().first;
int toCost = djikstra_pq.top().second;
djikstra_pq.pop();
int distanceToNextVertex = distanceV[toVertex];
if (distanceToNextVertex < toCost) {
continue;
}
for (int i = 0; i < edgeList[toVertex].size(); i++) {
// 다음 인덱스로 가는 cost
int cost = edgeList[toVertex][i].second + toCost;
// 나를 통해 갈 다음 IDX
int nextIdx = edgeList[toVertex][i].first;
if (cost < distanceV[nextIdx]) {
distanceV[nextIdx] = cost;
djikstra_pq.push({ nextIdx,cost });
}
}
}
}
int main() {
cin >> n >> m;
for (int i = 0; i < m; i++) {
int temp1, temp2, temp3;
cin >> temp1 >> temp2 >> temp3;
edgeList[temp1].push_back({ temp2,temp3 });
edgeList[temp2].push_back({ temp1,temp3 });
}
int start, end;
cin >> start >> end;
distanceV.assign(n + 1, INF);
djikstraSolution(start);
cout << distanceV[end];
}