급하게임개발

최근에 본 코테에서 나온 문제인데 프로그래머스에서 알고리즘 문제를 출제하는 기업들의 단골 기출 문제인 듯 하다 실제로 다른 회사에서도 출제된 사례가 있었다.같이 제공되는 이미지도 많이 겹치는 것 같다.

내적의 개념과 응용을 코테에 녹인 문제 인거 같다. 기억이 잘 안나고 그림도 기억나는데로 그려서 올리겠다

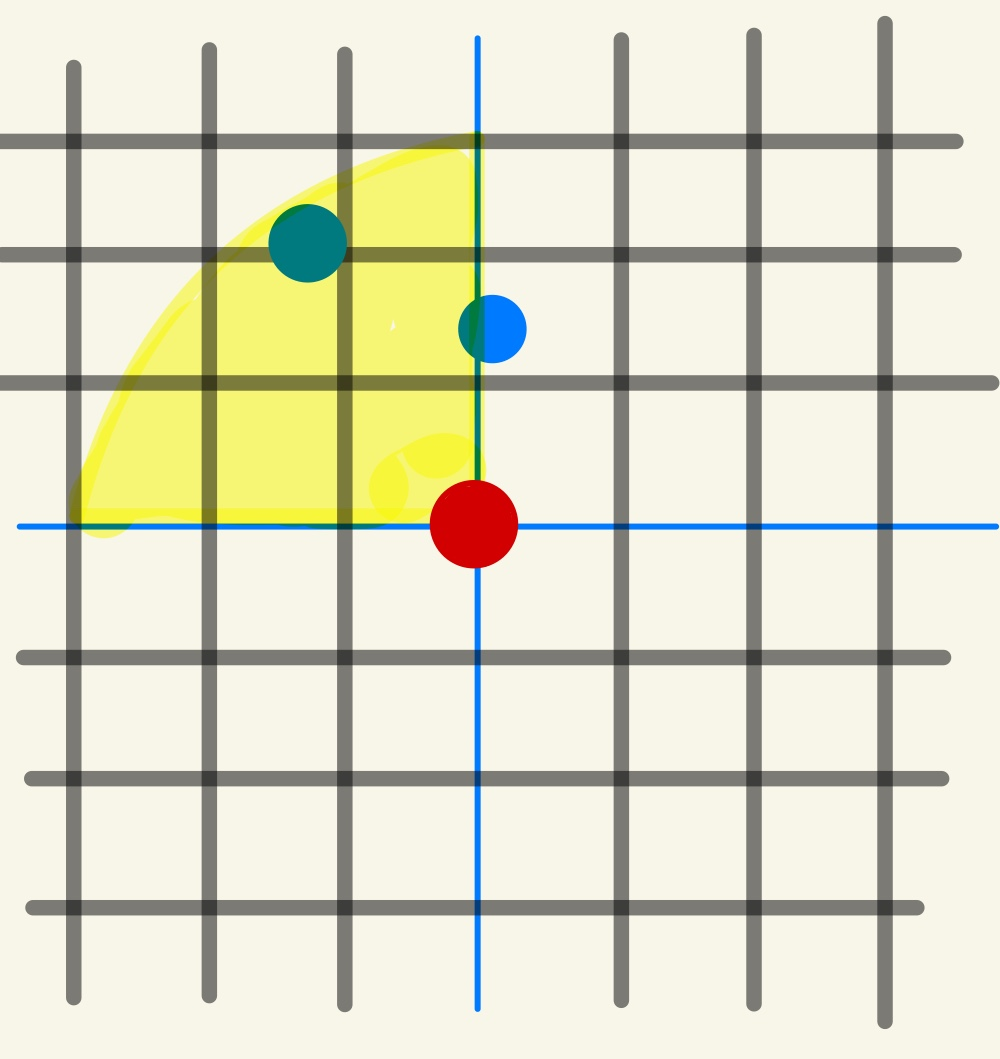
문제 :

한 게임의 캐릭터가 스킬을 사용한다.

해당 캐릭터가 스킬 사용시 스킬의 범위는 부채꼴이다.

해당 부채꼴 범위 안에 적이 있다면, 적은 데미지를 받지만, 범위 밖이라면 데미지를 받지 않는다.

데미지를 받는 적의 수를 Return하세요.

조건1 : 스킬을 사용하는 주체인 게임 캐릭터는 항상 0,0 위치에 있다.

조건2 : 적들은 0,0에 있을 수 없으며, 겹쳐있지 않다.

조건3 : 캐릭터와 일직선상에 적이 2명 이상 겹쳐있어도, 범위 안에만 들어오면 데미지를 받는 것으로 인식한다.

주어지는 값 : 

1. 스킬을 사용하기위해 위치해있는 마우스 좌표 int x,y

2. 스킬의 길이(반지름) int r

3. 각도 int d

4. 적들의 위치 xn, yn이 담긴 int형 2중벡터 vector<vector<int> > target

============================================================================================

이문제의 경우 나는 단계를 2개로 나눠서 풀 것이다. 1번 해당 적이 나를 기준으로 스킬범위 안에 있는가를 먼저 검증한다.

자 이 공식을 사용하면 된다. 어차피 우리는 좌표가 0,0이기 떄문에 실제로 해당 적의 x좌표의 제곱과 y좌표의 제곱을 더한것에 제곱근이 입력된 스킬의 길이보다 작으면 된다. 

또한 게임수학에서 내적은 두 벡터의 각도를 알려준다 이를 이용해 위에서 걸러낸 애들을 2차로 걸러준다. 이 때 우리가 사용할 함수는 acos()이다 이 함수의 경우 안에 내적으로 나온값을 넣어주면 우리가 원하는 각도의 값이 나온다 이를이용해 구현해보도록 하겠다.

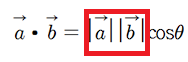
자 여기서 빨간 부분을 좌변으로 이항 시켜 보다 그럼 내적을 구하면 벡터의 크기의 곱으로 내적을 나무녀 cos인 값이 나오고 이를 acos에 넣으면 각도인 세타값이 나온다.

#include <iostream>
#include <cmath>
#include <vector>
using namespace std;
double Distance(double x, double y) {
	double distance;
	distance = sqrt(pow(x, 2) + pow(y, 2));
	return distance;
}

double  DotProduct(double x1, double y1, double x2, double y2) {
	return (x1 * x2) + (y1 * y2);
}

double sizeOfVector(double x, double y) {
	double size;
	size= sqrt(pow(x, 2) + pow(y, 2));
	return size;
}
int solution(int x, int y, int r, double d, vector<vector<int>>target) {
	int cnt = 0;
	for (int i = 0; i < target.size(); i++) {
		if (Distance(target[i][0], target[i][1])<=r) {
			if (acos(DotProduct(x, y, target[i][0], target[i][1]) / (sizeOfVector(x, y) * sizeOfVector(target[i][0], target[i][1])))<=d) {
				cnt += 1;
			}
		}
	}
	return cnt;
}
int main() {
	vector<vector<int>> target = { {1,3},{1,1},{4,3},{9,9},{-2,8} };
	cout<<solution(2, 4, 3, 60, target);
}

이를 코드로 작성하면 이렇게 된다.

이번에 모회사 코테를 보는 데 내가 못풀었던 문제에서 중복순열을 2번사용하여 경우의 수를 구하는 브루트포스 방식의 문제가 출제 되었던 거 같다. 내가 생각한게 정답이 아닐 수 도 있지만 적어도 내가 생각한데로 풀기 위해서는 중복순열과 순열을 구현했어야 했다. 하지만 오랫동안 기본적인 알고리즘 조차 손을 놓았어서. 역시 급하게 준비한 코테답게 불합격 메일을 기다리고 있다. 확실히 불합격이 되더라도 코테를 직접 보면서 어떤 식으로 공부해야할지 감이 잡히기 시작했다.

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
//중복 순열
int caseNum;
int arr[100000];
bool vectorIndexUsed[100000];
void DuplicatePermutation(int level, vector<int> caseVector) {
	if (level == caseNum) {
		for (int i = 0; i < caseNum; i++) {
			cout << arr[i];
		}
		cout << endl;
		return;
	}
	for (int i = 0; i < caseVector.size(); i++) {
		arr[level] = caseVector[i];
		DuplicatePermutation(level + 1, caseVector);
	}
}


void Permutation(int level, vector<int> caseVector) {
	if (level == caseNum) {
		for (int i = 0; i < caseNum; i++) {
			cout << arr[i];
		}
		cout << endl;
		return;
	}
	for (int i = 0; i < caseVector.size(); i++) {
		if (!vectorIndexUsed[i]) {
			vectorIndexUsed[i] = true;
			arr[level] = caseVector[i];
			Permutation(level + 1, caseVector);
			vectorIndexUsed[i] = false;
		}
	}
}

void Combination(int level, vector<int> caseVector, int beforeIndex) {
	if (level == caseNum) {
		for (int i = 0; i < caseNum; i++) {
			cout << arr[i];
		}
		cout << endl;
		return;
	}
	for (int i = beforeIndex; i < caseVector.size(); i++) {
		arr[level] = caseVector[i];
		Combination(level + 1, caseVector, beforeIndex + 1);
	}
}

int main() {
	cin >> caseNum;
	vector<int> dupPermuTest = { 1,4,5,2 };
	DuplicatePermutation(0, dupPermuTest);
	cout << "====================================="<<endl;
	Permutation(0, dupPermuTest);
	cout << "====================================="<<endl;
	sort(dupPermuTest.begin(), dupPermuTest.end());
	Combination(0, dupPermuTest, 0);
}

일단 기억나는 것은 주어진 벡터에서 몇명을 뽑아야하는 것이었다 이에 나는 중복순열,순열,조합순으로 현재 구현했다.

void DuplicatePermutation(int level, vector<int> caseVector) {
	if (level == caseNum) {
		for (int i = 0; i < caseNum; i++) {
			cout << arr[i];
		}
		cout << endl;
		return;
	}
	for (int i = 0; i < caseVector.size(); i++) {
		arr[level] = caseVector[i];
		DuplicatePermutation(level + 1, caseVector);
	}
}

중복 순열의 경우 똑같은 걸 여러번 사용해도 되니 굳이 사용했는지 안했는 지 체크할 필요가 없다

void Permutation(int level, vector<int> caseVector) {
	if (level == caseNum) {
		for (int i = 0; i < caseNum; i++) {
			cout << arr[i];
		}
		cout << endl;
		return;
	}
	for (int i = 0; i < caseVector.size(); i++) {
		if (!vectorIndexUsed[i]) {
			vectorIndexUsed[i] = true;
			arr[level] = caseVector[i];
			Permutation(level + 1, caseVector);
			vectorIndexUsed[i] = false;
		}
	}
}

순열의 경우 vector에서 순서가 다르면 다른것으로 인정하고 중복은 허하지 않는다

void Permutation(int level, vector<int> caseVector) {
	if (level == caseNum) {
		for (int i = 0; i < caseNum; i++) {
			cout << arr[i];
		}
		cout << endl;
		return;
	}
	for (int i = 0; i < caseVector.size(); i++) {
		if (!vectorIndexUsed[i]) {
			vectorIndexUsed[i] = true;
			arr[level] = caseVector[i];
			Permutation(level + 1, caseVector);
			vectorIndexUsed[i] = false;
		}
	}
}

조합은 중복을 허하지도 않고 순서가 달라도 같은 수를 뽑았으면  허용치 않는다.

void duplicateCombination(int level, vector<int> caseVector, int beforeIndex) {
	if (level == caseNum) {
		for (int i = 0; i < caseNum; i++) {
			cout << arr[i];
		}
		cout << endl;
		return;
	}
	for (int i = beforeIndex; i < caseVector.size(); i++) {
		arr[level] = caseVector[i];
		duplicateCombination(level + 1, caseVector, i);
	}
}

중복 조합은 같은 수를 뽑을 수 있고 순서가 존재한다 이에 같은수는 뽑을 수 있지만 순서가 다르고 동일한 요소로 이루어져있는 것은 이전에 뽑은것과 같음으로 허용치 않는다

이 정도 문법은 꼭 기억하도록 하자

https://www.acmicpc.net/problem/1759

이 문제는 일단 백준상에서 골드 5로 되어있는 문제다 근데 이문제를 보았을 때 느낀게 과연 내가 이 문제가  백트래킹인걸 모르고 풀었을 때 빠르게 정답을 유추 할 수 있었을까? 절대 아니다. 요즘 해당 알고리즘이 주어질 경우에는 그 알고리즘으로 문제를 빠르게 풀지만 내가 어떤 문젠지를 모르면 풀 수 있을 지는 모르겠다. 확실히 실무를 보다보니 머릿속에 생각한 것을 그대로 구현하는 구현능력은 조금 올라갔는데 앞으로도 계속 좋은 일이 있었으면 좋겠

#include <iostream>
#include <algorithm>
using namespace std;
int N, M;
char arr[16];
char answer[16];
int cnta;
int cntj;
bool isPassword;
int solution(int level, int beforeindex) {
	if (level == N) {
		cnta = 0;
		cntj = 0;
		isPassword = false;
		for (int i = 0; i < N; i++) {
			if (answer[i] == 'a' || answer[i] == 'e' || answer[i] == 'i' || answer[i] == 'o' || answer[i] == 'u')
			{
				cnta++;
			}
			else
				cntj++;
			if (cnta > 0 && cntj > 1) {
				isPassword = true;
				break;
			}
		}
		if (isPassword) {
			for (int i = 0; i < N; i++) {
				cout << answer[i];
			}
			cout << endl;
		}
	}
	else {
		for (int i = beforeindex + 1; i <= M; i++) {
			answer[level] = arr[i];
			solution(level + 1, i);
		}
	}
	return 0;

}
int main() {
	cin >> N >> M;
	for (int i = 1; i <= M; i++) {
		cin >> arr[i];
	}
	sort(arr+1,arr+M+1);
	solution(0, 0);

}

이코드의 경우 모음의 개수를 세주는 CNTA 자음의 개수를 세주는 CNTJ라는 변수가 존재 한다 이 변수의 경우 루프를 돌다가 특정 조건을 만족했을 때 바로 루프를 탈출하게 해준다. 즉 최종 4글자 가 모였을 때 이 문자열이 모음이 1개이상 자음이 2개이상이면 더이상 조건을 판단할 필요없으니 루프를 탈출하게 해주는 것이다.

	else {
		for (int i = beforeindex + 1; i <= M; i++) {
			answer[level] = arr[i];
			solution(level + 1, i);
		}
	}

이 부분의 경우는 재귀를 이용해서 백트래킹을 하기 위함인데 정렬되어있는 arr값에서 자기 이전의 index보다 큰 인덱스 부터 시작하기에 무조건 오름차순이 된다.

이 문제의 경우 기초적인 BFS문제 이다 일단 이문제가 원하는 건 경로가 아닌 루트의 갯수를 원하는 것이다. 이에 나는 평균적인 성능을 보장해 주는 BFS를 사용하였다.

#include <iostream>
#include <vector>
#include <queue>
using namespace std;

vector<int> bfsV[1001];
queue<int> bfsQ;
int arr[1001] = { 0, };
int N, M;
int cnt = 0;
int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);
	cin >> N >> M;
	for (int i = 0; i < M; i++) {
		int temp1, temp2;
		cin >> temp1 >> temp2;
		bfsV[temp1].push_back(temp2);
		bfsV[temp2].push_back(temp1);
	}
	for (int i = 1; i <= N; i++) {
		if (arr[i] == 0) {
			bfsQ.push(i);
			arr[i] = cnt;
			cnt++;
			while (!bfsQ.empty()) {
				int temp3;
				temp3 = bfsQ.front();
				bfsQ.pop();
				for (int j = 0; j < bfsV[temp3].size(); j++) {
					if (arr[bfsV[temp3][j]] == 0) {
						bfsQ.push(bfsV[temp3][j]);
						arr[bfsV[temp3][j]] = cnt;
					}
				}
			}
		}
	}
	cout << cnt;
}

https://www.acmicpc.net/problem/2630

처음에 이문제를 보았을 때 분할 정복을 사용해서 풀면은 될거같다는 느낌을 팍팍 풍기는 그림이 그려져 있었다.

이에 분할정복을 처음 사용 할때 나는 파란종이와 흰종이를 구하는 함수 2개를 만들어서 실행시켰다. 하지만 실행 시키고나니 시간초과가 발생하였다. 이에 시간 초과를 발생시키지 않기 위해서 파란색 종이를 구하면서 하얀색 종이를 구할 수 있도록 작성했다

#include <iostream>
using namespace std;
int N;
int bCnt;
int wCnt;
int arr[128][128];
int bSolution(int x, int y , int size) {
	if (size == 0) {
		return 0;
	}
	int check=0;
	for (int i = x; i < x+size; i++) {
		for (int j = y; j < y+size; j++) {
			if (arr[i][j] != 1) {
				check = 1;
				break;
			}
		}
		if (check == 1)
			break;
	}
	if (check == 1) {
		for (int i = x; i < x + size; i++) {
			for (int j = y; j < y + size; j++) {
				if (arr[i][j] != 0) {
					check = 2;
					break;
				}
			}
			if (check == 2)
				break;
		}

	}
	if (check == 0) {
		bCnt++;
	}
	else if (check == 1) {
		wCnt++;
	}
	else {
		bSolution(x, y, size / 2);
		bSolution(x, y + size / 2, size / 2);
		bSolution(x + size / 2, y, size / 2);
		bSolution(x + size / 2, y + size / 2, size / 2);
	}
	return 0;
}

int main() {
	cin >> N;
	for (int i = 0; i < N; i++) {
		for (int j = 0; j < N; j++) {
			cin >> arr[i][j];
		}
	}

	bSolution(0, 0, N);
	cout << wCnt<<endl;
	cout << bCnt << endl;
}

위에 코드를 보면 check라는 변수가 존재 한다 나는 check가 0일 때는 파란색종이의 갯수를 구하다 check가 1로바뀌면 흰종이를 check가 2로 해당영역이 파란종이도 흰종이도 아닌것이라고 파악했다 이경우 분할을 통해 다시 색종이의 갯수를 구한다.

	for (int i = x; i < x+size; i++) {
		for (int j = y; j < y+size; j++) {
			if (arr[i][j] != 1) {
				check = 1;
				break;
			}
		}
		if (check == 1)
			break;
	}

이부분은 해당영역에 0이 하나라도 있으면 break 한다 그럼 일단 파란종이는 아니다

	if (check == 1) {
		for (int i = x; i < x + size; i++) {
			for (int j = y; j < y + size; j++) {
				if (arr[i][j] != 0) {
					check = 2;
					break;
				}
			}
			if (check == 2)
				break;
		}

	}

이부분은 일단 파란종이가 아니니 흰종이인지 검사한다 이부분에서 0이 하나라도 발견되면 흰종이가 아니니 이제 모드를 check2로 바꾸고 분할정복을 시행한다. 확실히 회사일을 하다보니 알고리즘 실력은 줄었으나 뭔가를 생각하고 구현을 하는 능력은 올라간거 같다

https://www.acmicpc.net/problem/12865

이 문제는 내가 지금 까지 DP배열을 1차원 배열로 만드는데 익숙 해져서 그런지 2차원 배열로 설정 하는 것을 생각을 못해서 어려운 문제 였다. 이 문제의 경우 나는 이렇게 생각 해주었다.

일단 나는 이문제를 1번 아이템 부터 4번아이템을 넣어준다고 가졍하였다 이문제에서 0은 어떠한 아이템도 안 넣었다고 생각해서 0이자 무게가 0이라고 생각을 했다 이렇게 생각하지 않으면 너무 헷갈렸다 그래서 1번을 넣었을 때 무게가 6이고 7인 경우에는 1을 넣었기 때문에 1의 무게인 13을 넣었다. 1을 넣었을 때 무게가 1,2,3,4 일 수는 없으니 1을 넣지 않았다는 표시이자 안 넣었고 무게도 0이니 0으로 한다. 2번아이템을 넣었을 때 도 마찬가지 무게가 1,2,일 때는 2번을 넣었을 때

무게가 4로 초과되니 0으로 표시한다 그후 무게가 4랑 5일때는 

나의 이전 단계인 1을 넣었을 때의 무게들 중 나를 안넣었다고 가정한 무게 + 나의 무게를 했을 때와 이전단계의 무게들과 비교하여 더큰 값을 넣어준다. 이것을  dp로 표현 하면

dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - W[i]] + V[i]); 

예시로 dp[2][6]은 dp[1][2]+v[2] 과 dp[1][6]일 때를 비교한다 이 의미는 1을 먼저 넣을 안넣을 지 결정하는 상태에서 무게가 2일때+나의 더했을 때의 가치와 1을 넣을 안넣을지 결정했을 무게가 6인 경우를 비교하여 더 큰 값을 선택한다.

쉽게 설명하자면

1을 넣을지 말지 결정했을 때  특정 무게를 맞춘다고 가정했을 때 나의 무게를 더해서 그 무게를 맞춘다고 가정한 값과 이전 단계에서 그 무게를 달성했을 때의 값을 비교하여 큰값을 선택해 주는것이다.

#include <iostream>
#include <algorithm>
using namespace std;
long long dp[101][100001];//가방 물건의 번호,내가방의 무게
int W[101];
int V[101];
int main() {
	int maxItemNum;
	int maxItemWeight;
	cin >> maxItemNum >> maxItemWeight;

	for(int i=1; i<=maxItemNum; i++){
		cin >> W[i] >> V[i];
	}

	for (int i = 1; i <= maxItemNum; i++) {
		for (int j = 1; j <= maxItemWeight; j++) {
			if (j - W[i]>=0) {
				dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - W[i]] + V[i]);
			}
			else {
				dp[i][j] = dp[i - 1][j];
			}
		}
	}
	cout << dp[maxItemNum][maxItemWeight];
}

그래서 이러한 점화식으로 이문제를 풀면 전체 식이 이렇게 된다. 1차원으로 dp를 세우는 거 뿐만 아니라 다차원의dp 도 세우는 방법을 연습해야 할거 같다.