급하게임개발

https://www.acmicpc.net/problem/1655

이 문제는 나의 부족한 머리로는 혼자 생각 할 수 없는 알고리즘이었다.

하지만 이번 문제를 푼 것을 계기로 똑같은 유형의 문제는 틀리지 않아야 겠다.

일단 풀이는 우선순위 큐 2개로 중간 값을 구하는 방법을 알아야 한다

이게 알파이자 오메가였다.

우선순위 큐로 2개의 값을 구하는 방법은

1. MaxHeap은 무조건 MinHeap보다 사이즈가 하나 커야 한다.

2. MaxHeap의 최대값은 MinHeap의 최솟값 보다 작아야 한다. 이 조건을 만족하지 않을 시

maxHeap의 최대값과 MinHeap의 최솟값을 swap해준다.

이 법칙을 지키면 MaxHeap의 최대값은 항상 중간값이 된다.

이 풀이를 위의 문제에서 주어진 예제에 대해서 대입해보겠다.

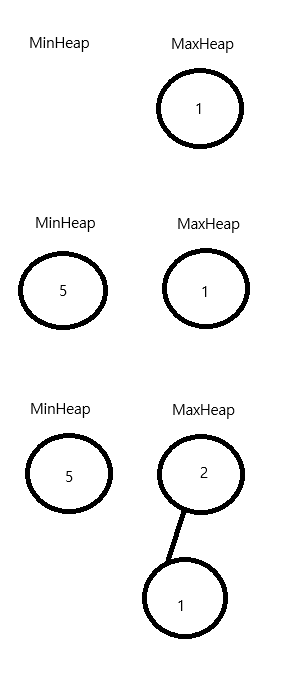
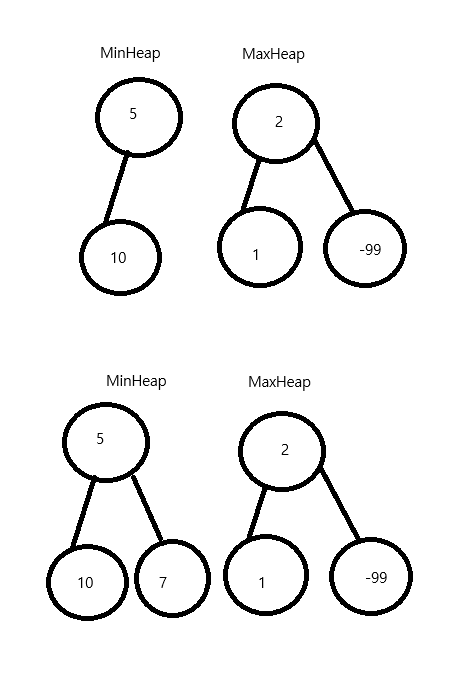
이런 순서대로 트리가 차면서 항상 Maxheap의 최대값이 중간값을 나타내고 있다. 

코드는 아래와 같다

#include <iostream>
#include <queue>
using namespace std;
priority_queue<int,vector<int>,less<int>> maxq;
priority_queue<int, vector<int>, greater<int>> minq;
int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);
	int N;
	cin >> N;
	int inputNum;
	cin >> inputNum;
	maxq.push(inputNum);
	cout << maxq.top() << '\n';
	for (int i = 1; i < N; i++) {
		cin >> inputNum;
		if (maxq.size() == minq.size())
			maxq.push(inputNum);
		else {
			minq.push(inputNum);
		}
		if (!maxq.empty() && !minq.empty() && !(maxq.top() < minq.top())) {
			int a = maxq.top();
			int b = minq.top();

			maxq.pop();
			minq.pop();

			minq.push(a);
			maxq.push(b);
		}
		cout << maxq.top()<<'\n';
	}
}

이 문제의 경우 나에게 여러가지 에러를 보여줌으로 여러가지 함수를 사용할 때 주의 할점을 알려줬다. 일단  이 문제의 코드는 이렇게 된다

#include <iostream>
#include <queue>
#include <vector>
#define INT_MAX 2147483647
using namespace std;
vector<int> distanceV(20002); //시작점 부터 다른 정점까지의 거리를 저장
vector<bool> visited;
void djikstra(int start, vector<pair<int, int>> dijkstraGraph[]) {
	priority_queue < pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq; // 거리, 노드 인덱스
	pq.push(make_pair(0, start));
	distanceV[start] = 0;

	while (!pq.empty()) {
		int distanceOfTo = pq.top().first;
		int toVertex = pq.top().second;
		pq.pop();

		if (distanceOfTo > distanceV[toVertex]) {
			continue;
		}

		for (int i = 0; i < (int)dijkstraGraph[toVertex].size(); i++) {
			int cost = distanceOfTo + dijkstraGraph[toVertex][i].second;
			int nextIndex = dijkstraGraph[toVertex][i].first;
			if (cost < distanceV[nextIndex]) {
				distanceV[nextIndex] = cost;
				pq.push(make_pair(cost, nextIndex));
			}

		}
	}
}
int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);
	int vertex, edge, start;  //vertex는 정점 edge는 간선 start는 시작점을 입력 받는다.
	cin >> vertex >> edge >> start;
	vector<pair<int, int>> dijkstraGraph[20002];//다익스트라 알고리즘의 비용을 저장할 우선순위 큐
	for (int i = 1; i <= edge; i++) {
		int from, to, cost;  //from은 간선사이의 시작점,to는 도착점 , cost는 간선의 비용을 의미
		cin >> from >> to >> cost;
		dijkstraGraph[from].push_back(make_pair(to,cost));
	}
	distanceV.assign(20002, INT_MAX);
	djikstra(start, dijkstraGraph);
	for (int i = 1; i <= vertex; i++) {
		if (distanceV[i] == INT_MAX) {
			cout << "INF"<<endl;
		}
		else {
			cout << distanceV[i] << endl;
		}
	}
}

이 문제의 경우 일단 간선의 방향이 단 방향이다. 일단 이문제의 예시 input에 대한 과정의 그림을 첨부하겠다

이 그림 에서 원으로 되어 있는 그래프는 위에 dijkstra함수에 pq를 그린것이다. 밑에 배열은 distanceV를 그린것이다.

일단 처음 풀이에서

distanceV.assign(20002, INT_MAX);

이 코드를 통해 배열에 큰 값을 다 넣어주었다 이에 처음 벡터에는 INF값만 가득하다 그후 1,0 즉 시작점 1에서 도착지 1로가는 거리는 자기자신이므로 0을 넣어준다 그후 2,2순으로 pq순에서 팝되는 값과 나와 연결되어 있는 다음 인덱스의 값을 더해서 distanceV에 거리를 갱신해 준다. 즉 1이 팝되었을때는 2,3의 거릿값이 갱신된다. 이후 2가팝되었을 때는 3과 4에 연결되어있으므로 시작점부터 자기자신까지의 거리와 나랑 연결되어 있는 노드의 값을 더해서 만약 원래 그 노드까지의 거리보다 나를 통해 가는 거리가 짧으면 그 노드쪽의 값을 갱신해주고 아니면 넘어간다 이런식으로 계속 나까지의 거리와 다음 노드까지의 거리를 계속 갱신해주면서 최소 거리를 구하면 된다.